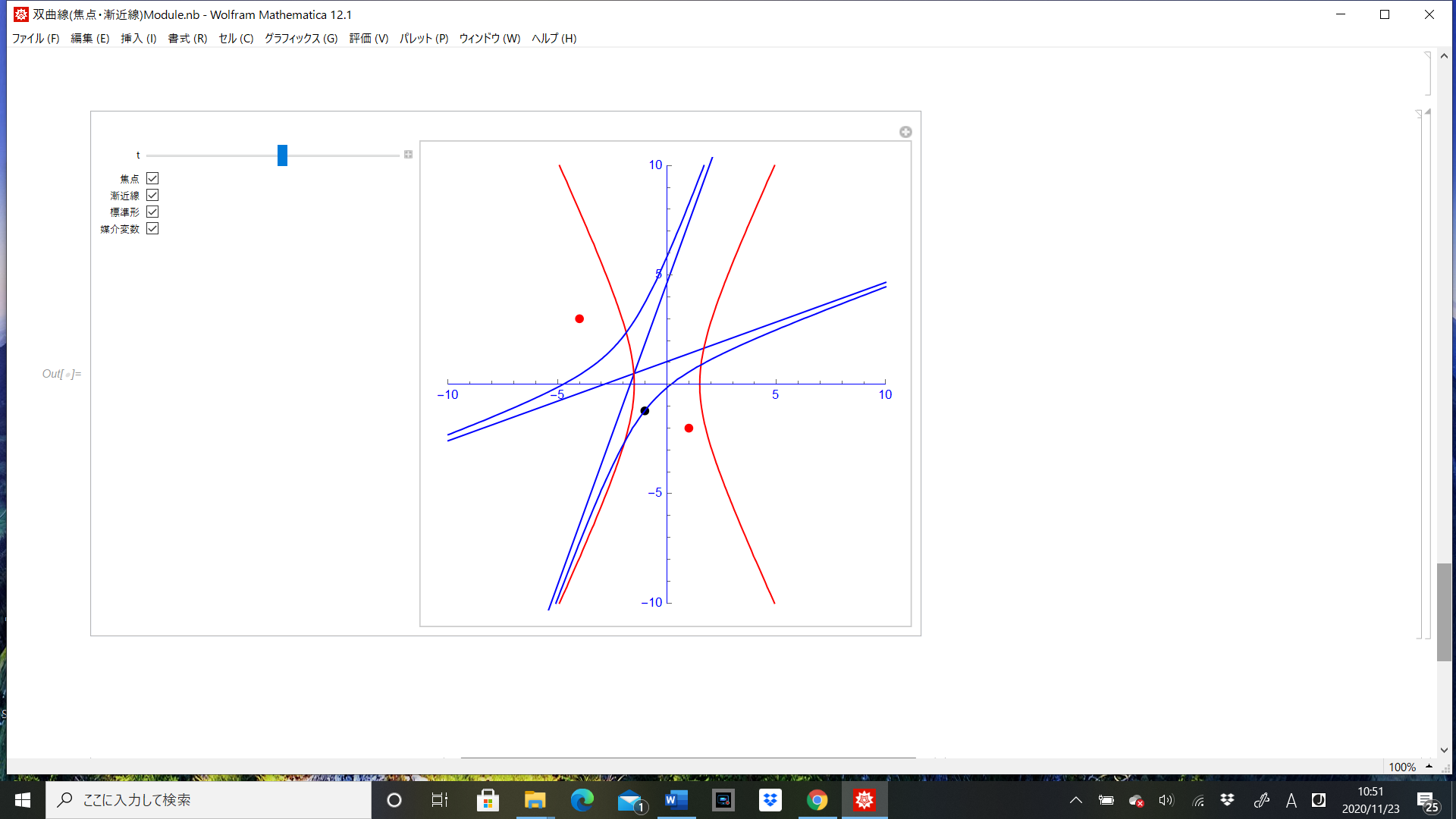
例えば曲線 y = x2 1xn は x→±∞において y = x2 に限りなく近づきますが,高校では漸近線として y = x2 を求める必要はありません。この例では, 縦線: x = 0 だけが漸近線です。 (A) 「縦」の漸近線の求め方 有限の値 a に対して, limx→alimiif (x) = ∞ または −∞ limx→−alimiif (x) = ∞ または −∞ となるとき (一方だけでもよい), x = a が漸近線です. この形の漸近線グラフを描くと,関數 f(x) = 1 / x のグラフである。 このグラフの漸近線は, y軸と平行な漸近線の求め方がわかりません。 答えは y= 1/2のようです。 解 雙曲線 1 雙曲線の方程式の標準形 ※雙曲線の方程式は,漸近線や焦點の求め方 ">Feb 04, 双曲線の漸近線の問題です。 正答率が528%と少し低いのは 漸近線の求め方を忘れてしまっていたか、 平行移動を逆にし Skip navigation

双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ
曲線 漸近線 求め方
曲線 漸近線 求め方-Double (inflec_pt) ans = 3×1 complex i 136 i 136 i この例では、最初の要素だけがB 距離の差 2 b 双曲線の y 軸との交点の y 座標の値は b, − b この双曲線を表す方程式は



曲線の漸近線について X軸に垂直な漸近線とありますが X軸に垂直な漸近線 Yahoo 知恵袋
②2つの焦点がy軸上にある双曲線 (x 2 /a 2)(y 2 /b 2)=1 のグラフの描き方はわかりましたね。a,bの値を求め,頂点の座標と漸近線から双曲線を描けばよいのです。仕上げに,焦点の座標の求め方を確認しておきましょう。F (x)xnnn = a とする。 ( a = 0 のときは x 軸に平行) この極限がなければ, x → ∞ のとき漸近線なし。 2) 1)の極限値が存在するとき, a の値を用いて, limx→∞limii {f (x)−ax} = b とする. ※ 横 ( x 軸に平行)の漸近線は,直ちに見つかることがあります。 例 y = e −x2 のとき limx→∞limii e −x2 = 0 だから y = 0 は漸近線です. 上の議論で a = 0, b= 0 です。 ※ ( y = ±f (x) のInflec_pt = solve (f2, 'MaxDegree' ,3);
B a x となる. ページトップへ 双曲線の定義(焦点がy軸上の場合) F 1 (c, 0) F 2 (− c, 0) F 1 P = x 2 y − c 2 F 2 P = x 2 y − (− c) 2 F 1 P − F 2 P = 2 b c >Oct 23, 18曲線がある直線に限りなく近づいていくとき、その直線のことを漸近線(asymptote) と言います。漸近線は、基本双曲線と漸近線や基本一次分数関数のグラフなどでも出てきていますが、このページの後半で、もう少し詳しく見ることにしましょう。双曲線の焦点の求め方 作成者 Bunryu Kamimura (1)共役直径から軸を見つけ、中心を見つける (2)擬似的な漸近線を引く(これがすっきりしない) (3)頂点から軸と直交する線を引いて交点を通る円を描
2 a, 0) (\pm\sqrt{2a},0) (±漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) lim3 漸近線の求め方 31 軸に平行な漸近線の求め方 32 軸に平行でない漸近線の求め方2STEP 321 STEP1 の極限を調べる→傾きチェック 322 STEP2 代入する 4 漸近線の有無の判別方法 41 チェック① 軸に平行でない漸近線があるか 42 チェック② 不連続な点が



漸近線 Op Twitter




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
数学・算数 2次曲線 双曲線 X²-Y²/9=1→(x²-9分のY²=1) の焦点と漸近線の方程式の求め方、さらにP1(2、3√3)における接戦の方程式の求め方をおしえてください。 質問NoMay 08, 21漸近線を見出すことは、曲線の概形をつかむ一助となる。 特に、座標平面における関数に対しては、そのグラフの漸近線の方程式は(存在の可否も含めて)求め方が確立されている。関数のグラフの接線の極限が存在するならばそれは漸近線に等しい 。漸近線とはグラフが近づいていく直線(または曲線)のことです。 厳密には極限を用いて定義されますが,一次分数関数に関しては漸近線は極限の議論をしなくても分かります。 さきほどかいた二つのグラフを見れば明らかでしょう。 一次分数関数 y −



曲線の漸近線について X軸に垂直な漸近線とありますが X軸に垂直な漸近線 Yahoo 知恵袋



微分をしてグラフを描く問題で確認するポイント 数学 微分 そーまのブログ屋さん
Oct 25, C;4 xy^238 y357=0 高1までに學ぶ 易しい 放物線 を定める。 F(x,y)=((4/(4 x2 y^238 y)),(2 y38)/(4 x2 y^238 y))なる 非線型写像による C の像を 多様な発想で 求めて もし Fが 双曲線なら 漸近線を多様な発想で求めて F と共に図示し 共軛な双曲線をも 図示願います; 不定方程式 の解集合 F∩Z^2 の2 a , 0) a <0 a <0 a <




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




漸近線方程
漸近展開に関するメモ 漸近展開に関するメモ Landau の記号と漸近展開 ver13 京都府立鳥羽高校定時制 稲葉芳成 はじめに この文章は, 大学初年度向けの微分積分のテキストである, 「三宅敏恒著『入門微分積分』培風館」を参考にして, 内容が平易で漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、 $$\lim\lim_{x \to \infty}\{f(x)(axb)\}=0$$ が成立します。 これは、教科書に載っていない場合もあるみたいですが、通常漸近線とくればこのように定義されます。Sep 16, 『曲線 x^3+y^3-1-xy=0 の漸近線 3x+3y+1=0 を如何にして求めるか?』シリーズの最終回です. 図を見てください. ぽっこりカワイイ曲線は,45°回転すると,真横を向いたポッコリ曲線に変わりそうです.では,回転はどうとらえましょう? 点P(p,q)を原点のまわりに45°回転して得られる点
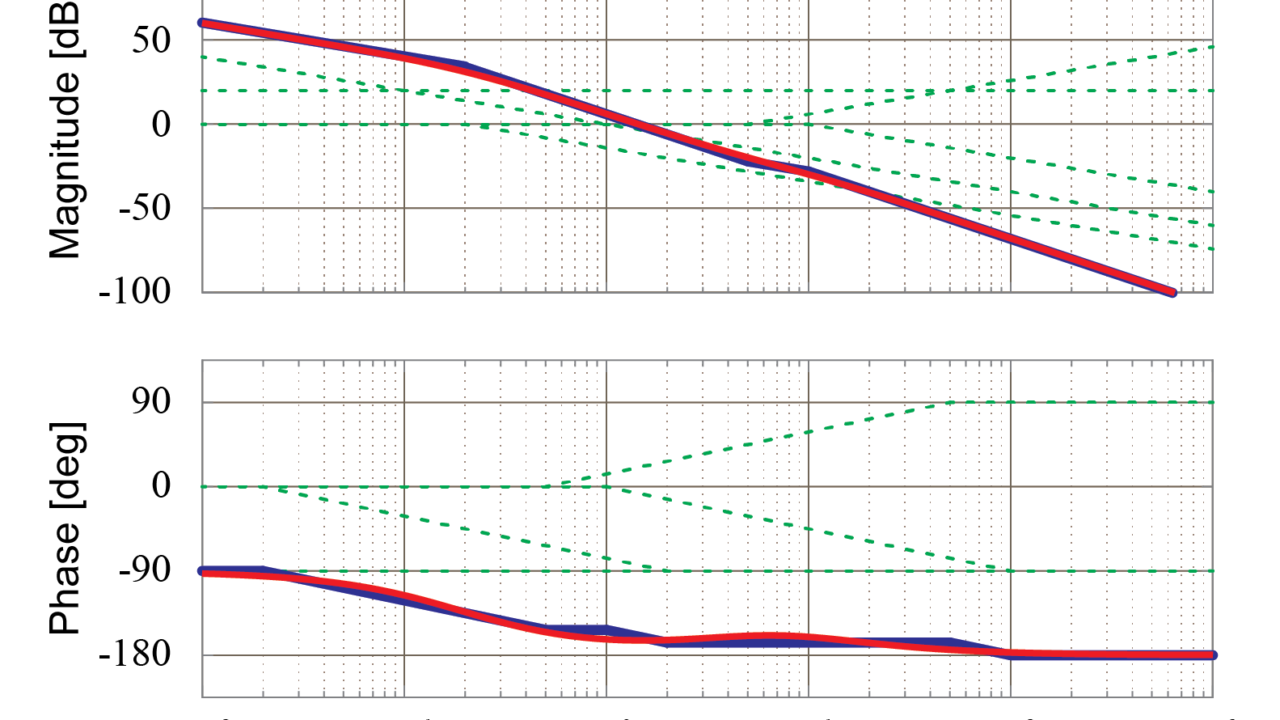



実際に伝達関数からボード線図を漸近線近似で書いてみよう その3 Tajima Robotics




漸近線の求め方 高校数学 微分法の応用 14 Youtube
例えば,直線 =c が曲線 =f( ) の漸近線に なるとする。曲線 =f( ) 上の点P( ,f( ))が 直線 =c に近づくことから, c0 または c−0と考える。点Pが無限遠に遠ざかること から,OP = f( ) ∞が成り立つので,これ らを合わせると, limしたがって, y = ±Dec 09, 05そこで、双曲線の頂点といったらいいのか・・・ 呼び方はわかりませんが、グラフを書くときに(2,3)を中心とした四角いボックスをかいて、そこの辺に接するように双曲線の頂点を書き、ボックスの対角線上に漸近線がくるように書く。




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典
Y x=\pm y x = ±グラフ,漸近線 デカルトの葉線のグラフは図の青い曲線になります。 グラフは y = x y=x y = x に関して対称です。 (x, y) (x,y) (x, y) が x 3 y 3 − 3 a x y = 0 x^3y^33axy=0 x 3 y 3 − 3 a x y = 0 を満たすなら, (y, x) (y,x) (y, x) も満たすことから分かります。 また, y = − x − a y=xa y = − x − a を漸近線に持ちます。Mar 06, 21双曲線の漸近線の公式を証明する前に「漸近」という意味をきちんと数式で表しておきます。 x → ∞ x\to\infty x → ∞ での漸近線: lim x → ∞ ∣ f ( x ) − g ( x ) ∣ = 0 \displaystyle\lim_{x\to\infty}f(x)g(x)=0 x → ∞ lim ∣ f ( x ) − g ( x ) ∣ = 0 が成立するとき, f ( x ) f(x) f ( x ) は g ( x ) g(x) g ( x ) に漸近すると言う。




漸近線




高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット
B a x 1 − 0 より, x 2 a 2 − y 2 b 2 = 1 の漸近線は y = ±Upcoming Cancel Play Now You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your2 双曲線上の点から つの焦点までの距離の差は d( 3) 3) d ) 3 漸近線は 直線 \ e d ,\ e d 4 曲線は 軸,\ 軸,原点 2 に関して対称 本の漸近線の方程式は d \ e , d \ e と表すことができる。 平面上の曲線2次曲線 7 \ (
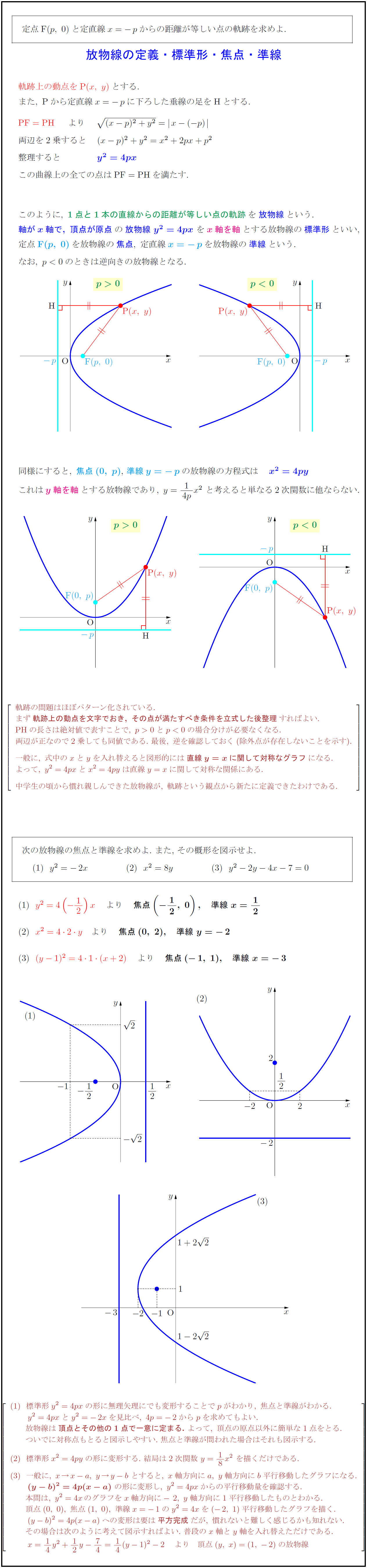



高校数学 放物線の定義 標準形 焦点 準線 受験の月




漸近 線 求め 方 漸近線の求め方を解説しました
Oct 22, いただいた nb を見て、漸近線の求め方の別解?も「2次曲線について4.」としてブログにあげさせてもらいました。ありがとうございます。 整数解の方は、Wolfram alpha に解かせたところ、無限個あるようですね。Nov 23, 12曲線の漸近線の方程式の求め方。 数Ⅲの微分です。 高校数学 漸近線 数3 青チャート 画像の問題の(2)の解答の2行目のところに「定義域ではこの関数は連続であるから、x軸に垂直な漸近線はない」とありますが、なぜそのように言えるのですか?双曲線 1 双曲線の方程式の標準形 ※双曲線の方程式は,中学校で反比例のグラフ y= において登場するが,そこでは直角双曲線だけを扱った.以下においては,必ずしも漸近線が直角に交わらない一般の




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
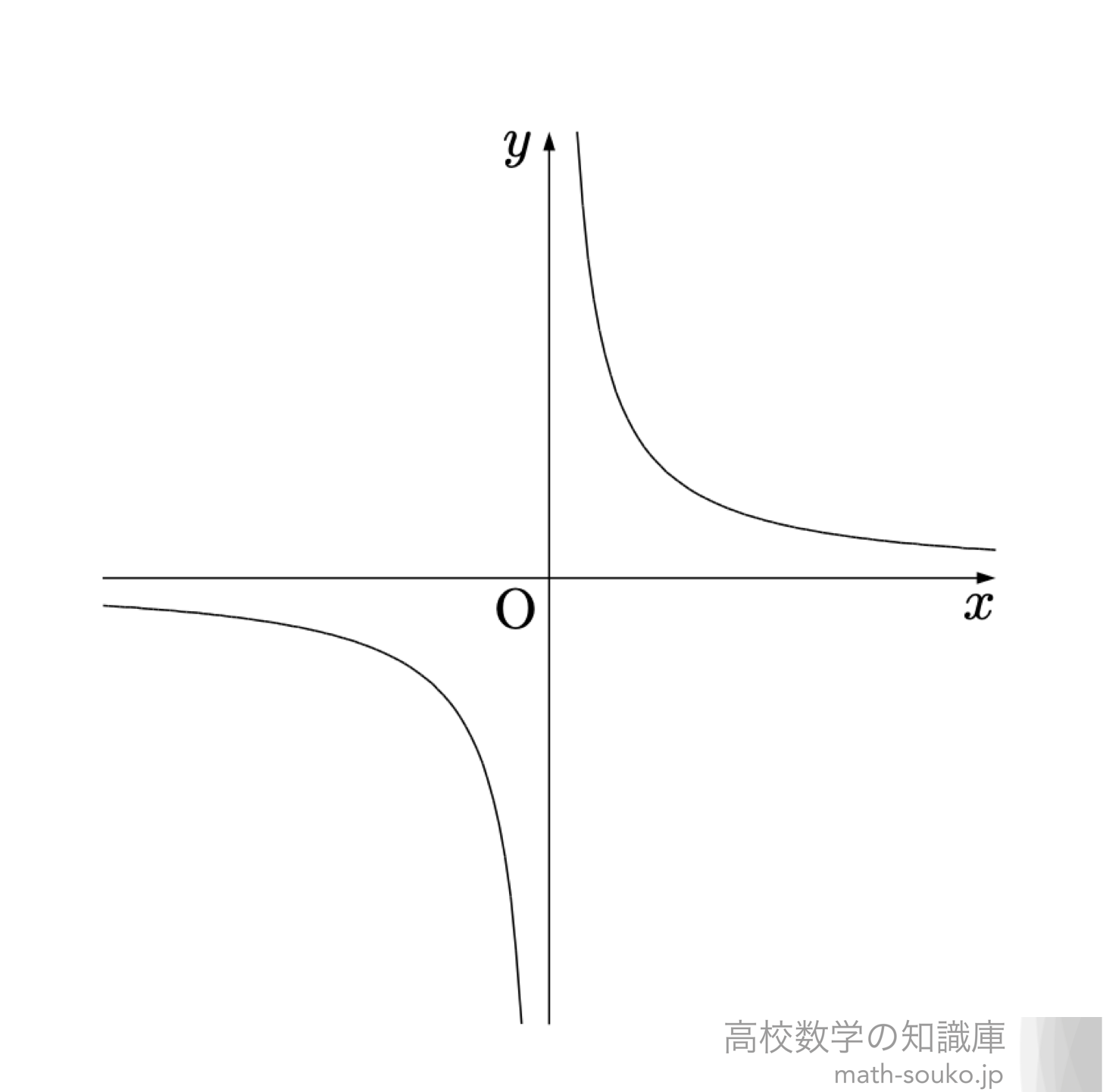



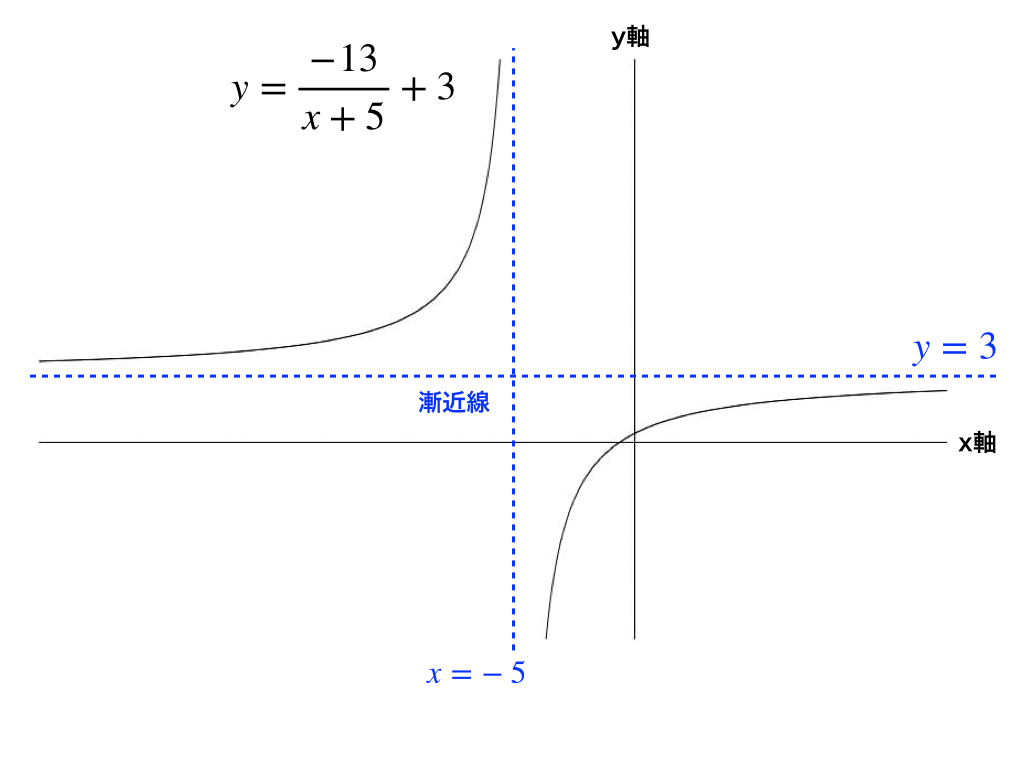
分数関数のグラフ 反比例と平行移動 高校数学の知識庫
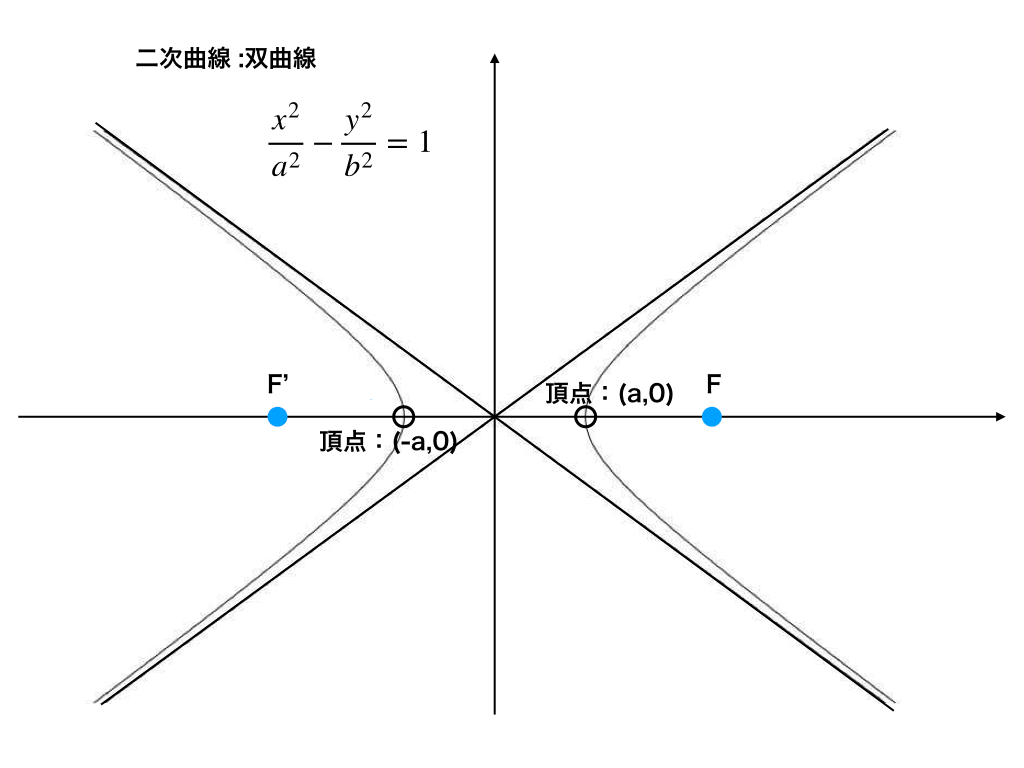
変曲点を求める の変曲点を求めるには、2 次導関数を 0 に等しくなるように設定して、この条件を解きます。 f2 = diff (f1);双曲線の漸近線の簡単な求め方と証明 双曲線の漸近線: パターン1.双曲線 x 2 a 2 − y 2 b 2 = 1 \dfrac{x^2}{a^2}\dfrac{y^2}{b^2}=1 a 2 x 2 − b 2 y 2 = 1 の漸近線は正葉線 この曲線は、デカルトの正葉線といわれ、漸近線を有する。 方程式 の媒介変数表示をいろいろ工夫して求めてみよう。 (単純に、と置いては失敗する! いま、与えられた方程式を次のように変形する。 すなわち、 ここで、と置き、さらに y を消去して、次のような2次方程式を得る。 これを、解の公式を用いて解けば、



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




高校数学 双曲線の接線と漸近線に関する有名性質 受験の月
Nov 29, 14数学 (e^2x1) / (e^x2) の漸近線を求めよという問題があります。 xはわかったのですが、 y軸と平行な漸近線の求め方がわかりません。 答えは y= 1/2のようです。 解May 06, 09双曲線について x^2/a^2y^2/b^2=1 焦点の座標を(c,0)(c,0) 漸近線;y=bx/a だとします。 c=√(a^2b^2)となるのは何故でしょうか? 手元にはグラフがあるのですが、これが導けません・・。 よろしくお願い致します。Nov 02, (グラフの準備:漸近線の求め方(分数関数)) 3333(グラフの準備:漸近線の求め方(無理関数)) 3334(グラフの準備:漸近線の求め方(指数対数関数)) 3335(y"の正負はグラフの凹凸を表す) 3336(変曲点とy"の符号) 3340(分数関数のグラフ) 3341(グラフの合成②)




漸近線の意味 用法を知る Astamuse




Y Ax B 2x 1 1 のグラフが点 1 0 Okwave
X 2 − y 2 = a x^2y^2=a x 2 − y 2 = a の漸近線は x = ±漸近曲線を求めるのはベクトル場が与えられたときの積分曲線,すなわち 微分方程式(5),(6) を解くことになる. 曲面上の曲線の法曲率とは,曲線の曲率ベクトルすなわちk(s)β(s) = dα(s) ds の接平面の法線ベクトル−→n への正射影であったから,法曲率を求めJun 30, 19微分のとこでグラフ描いてるんですけど漸近線の求め方が分からないです。 参考書に書いてある lim x → ∞ { f ( x) − ( a x b) } = 0 \displaystyle\lim_ {x\rightarrow\infty}\ {f (x) (axb)\}=0 x→∞lim {f (x)−(axb)}= 0 ってどういうこと? 確かにパッと見た目じゃ




次の曲線について 放物線なら頂点の座標 権円なら中心の座標 双曲線なら漸近 クァンダ Qanda で解き方を見る




高校数学 双曲線のグラフ 2 問題編2 映像授業のtry It トライイット
※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります. 例11
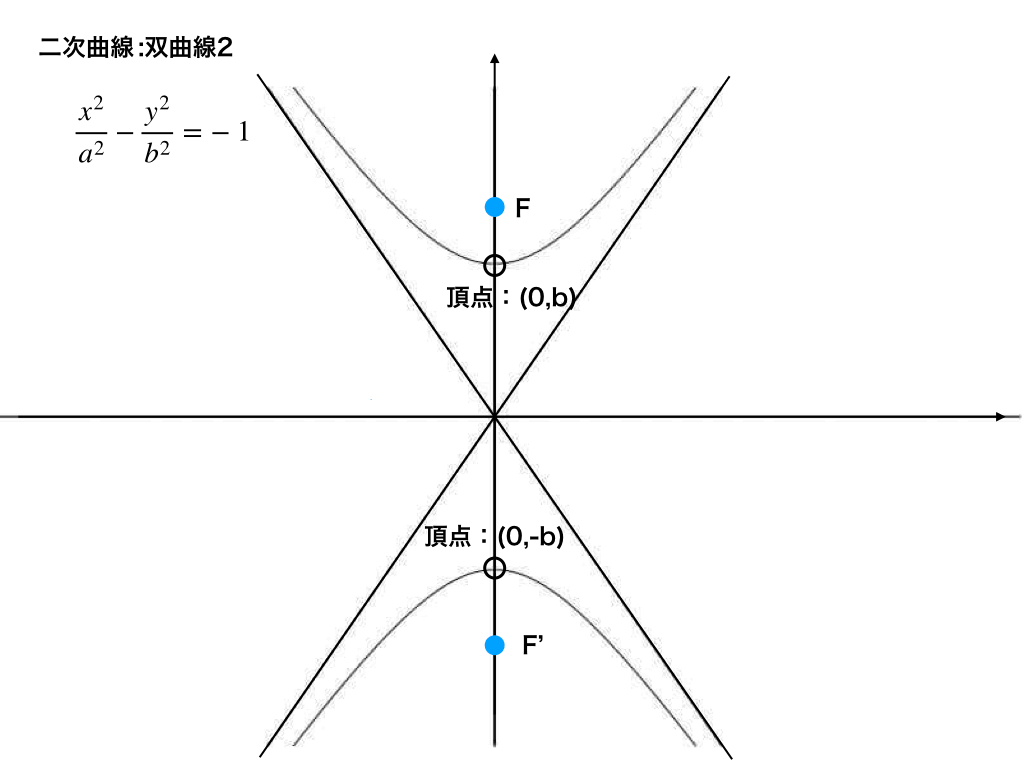



双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説



微分をしてグラフを描く問題で確認するポイント 数学 微分 そーまのブログ屋さん




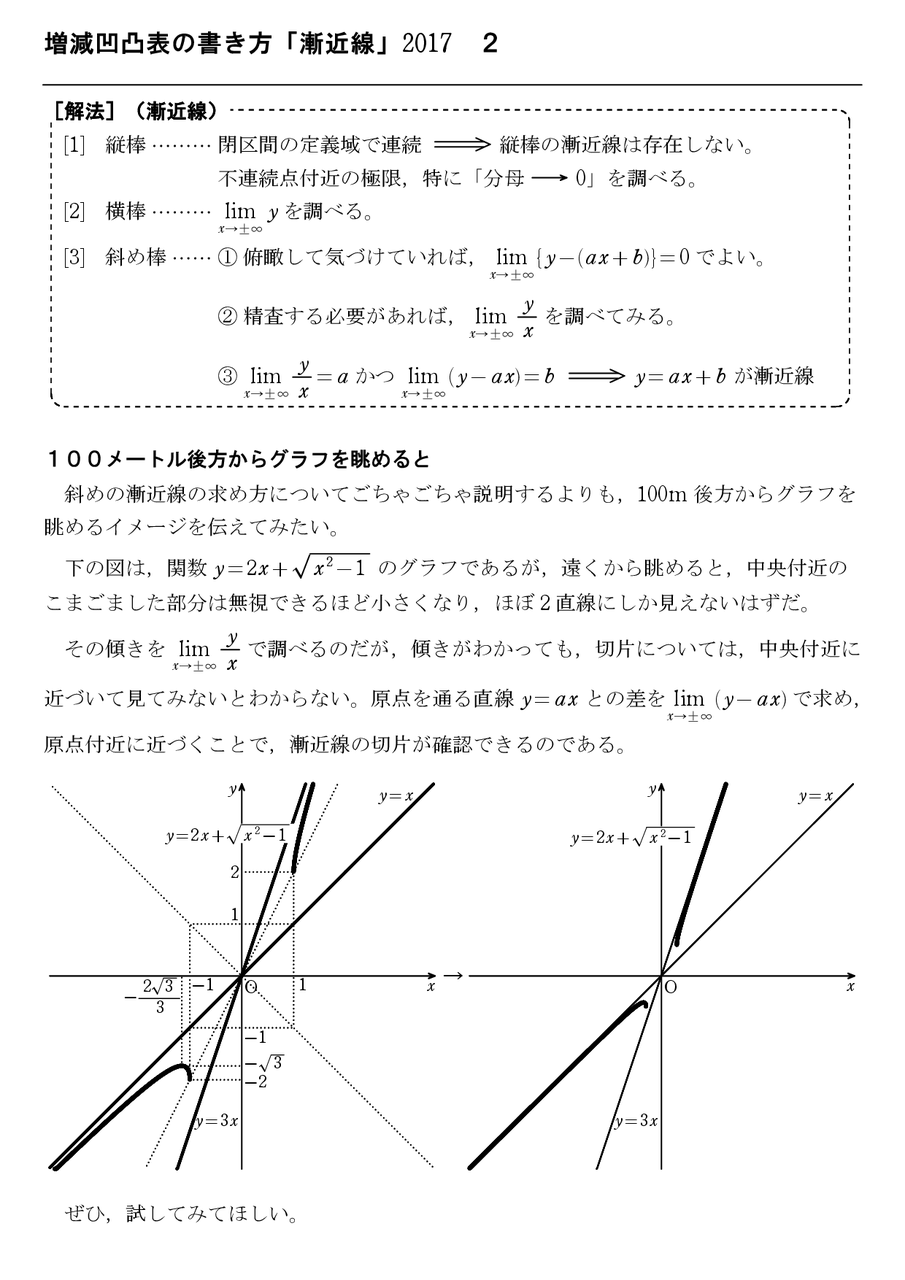
増減凹凸表を書く手順 7 漸近線 3 怜悧玲瓏 高校数学を天空から俯瞰する
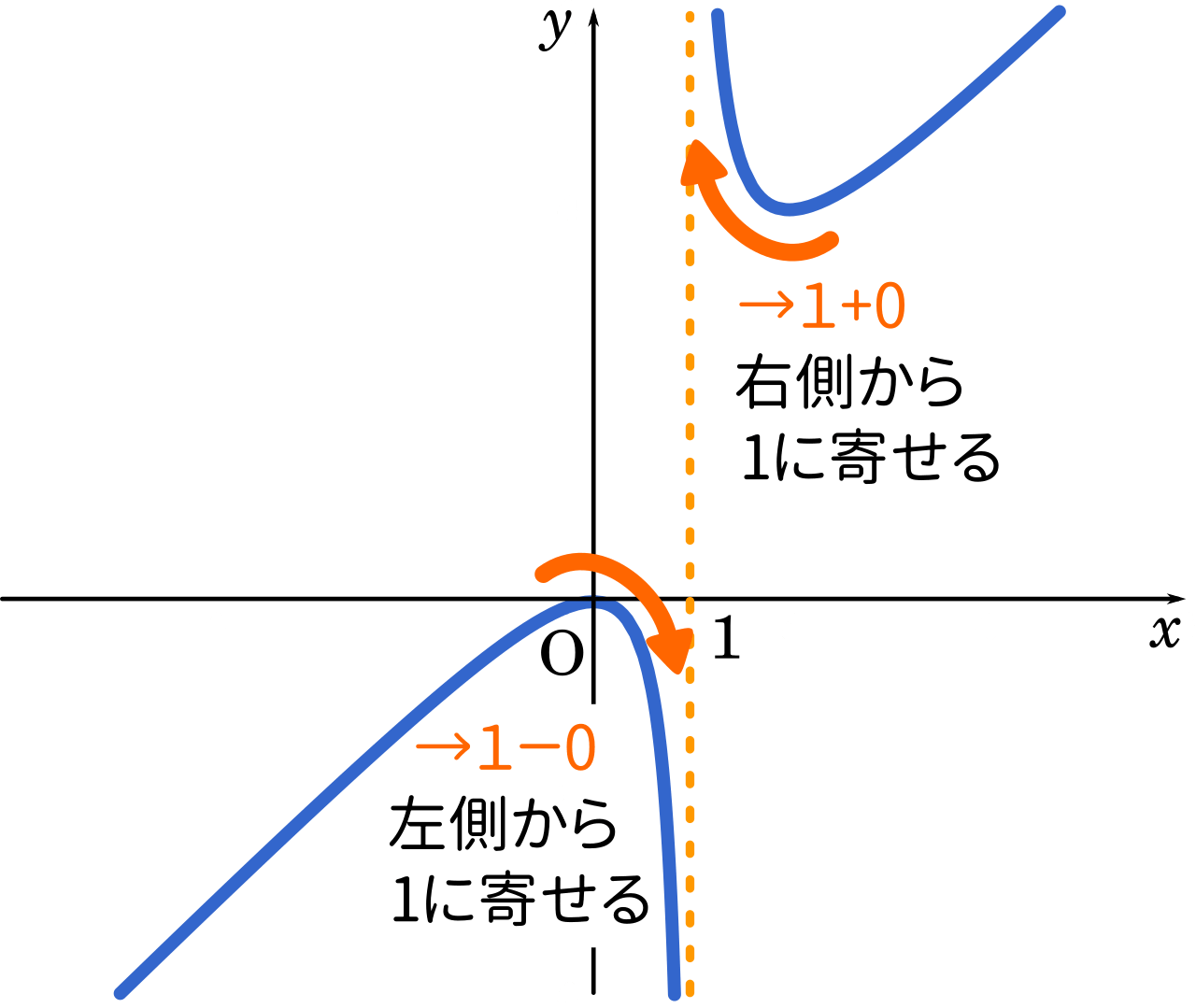



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書
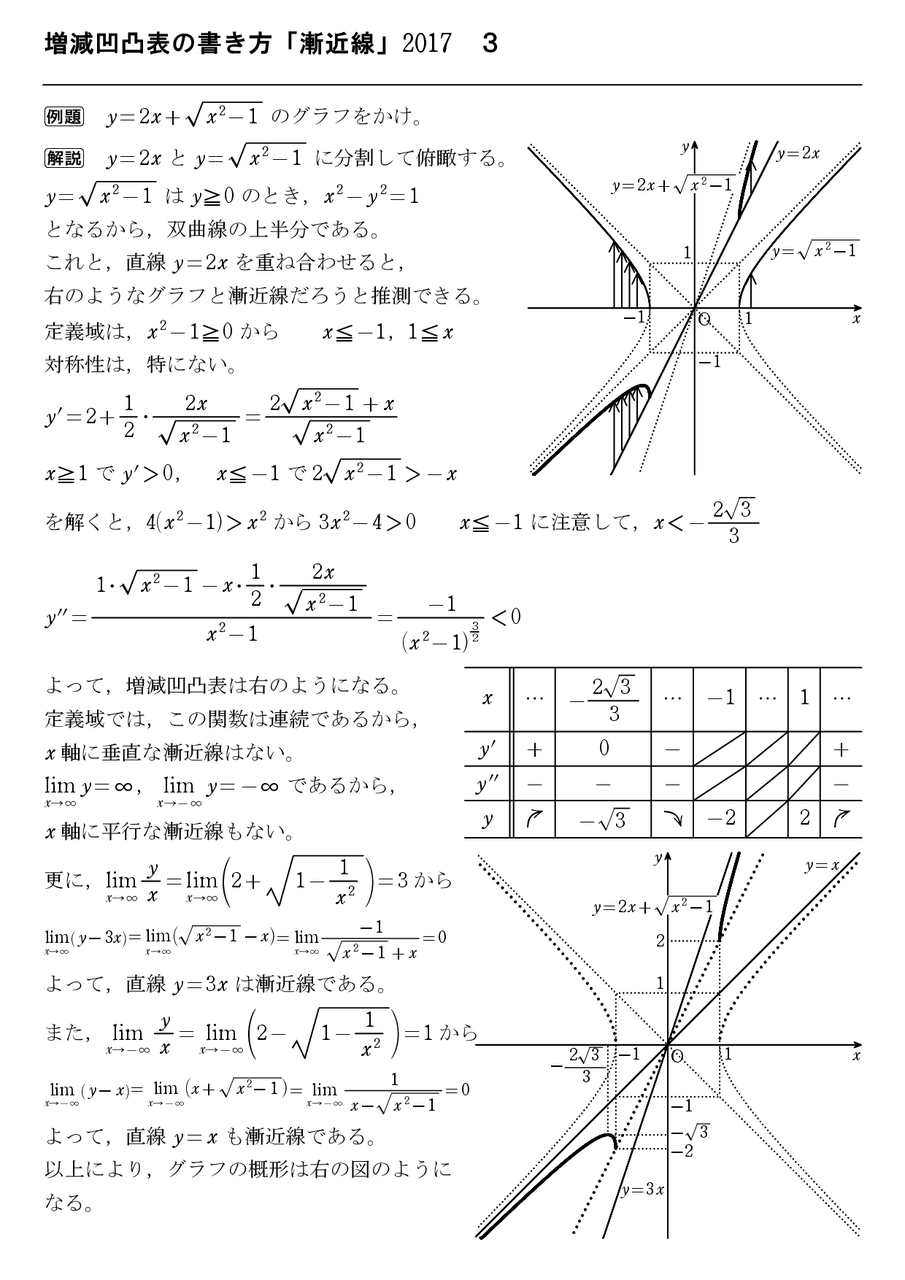



増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する




漸近 線 と は 数 微分の応用 ざっくりイメージから漸近線を導く




高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月




数3の グラフの凹凸と変曲点を求める問題での漸近線の求め方が あいうえおって何ってい Clear




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
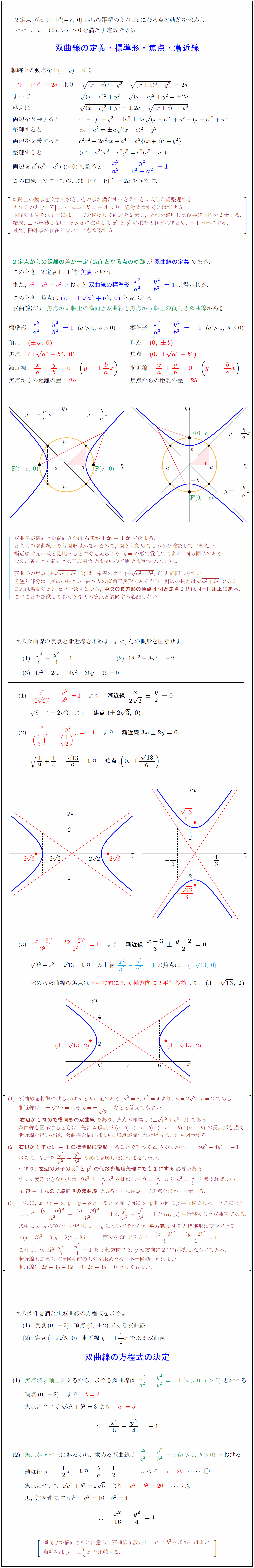



高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典



漸近 線 求め 方 漸近線の求め方を解説しました




高校数学 2次曲線の決定 2 問題編 映像授業のtry It トライイット



増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線 Op Twitter




分数関数のグラフと漸近線 高校数学 関数 1 Youtube




漸近線の求め方がこうなる理由がよく分かりません 下に書いてある証明 はどういう意味な Clear



双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説




高校 数学 式と曲線10 双曲線のグラフ1 分 Youtube




漸近線の求め方がこうなる理由がよく分かりません 下に書いてある証明 はどういう意味な Clear



曲線の漸近線について X軸に垂直な漸近線とありますが X軸に垂直な漸近線 Yahoo 知恵袋




分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




漸近線の求め方が分かりません 3 です Clear




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
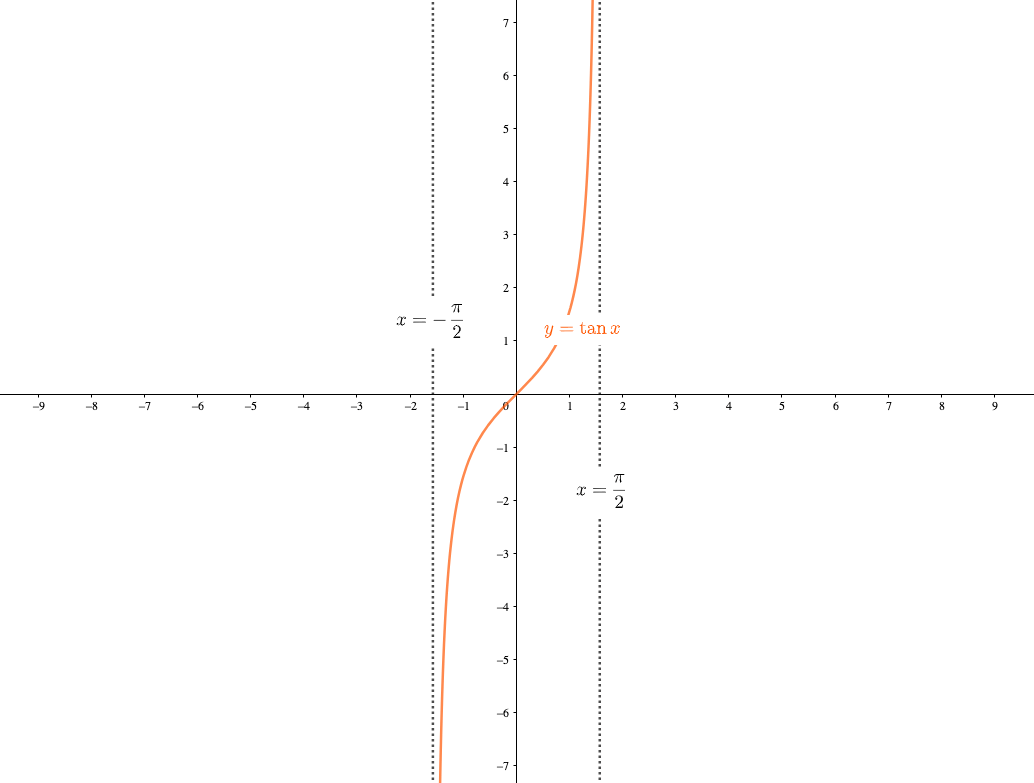



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
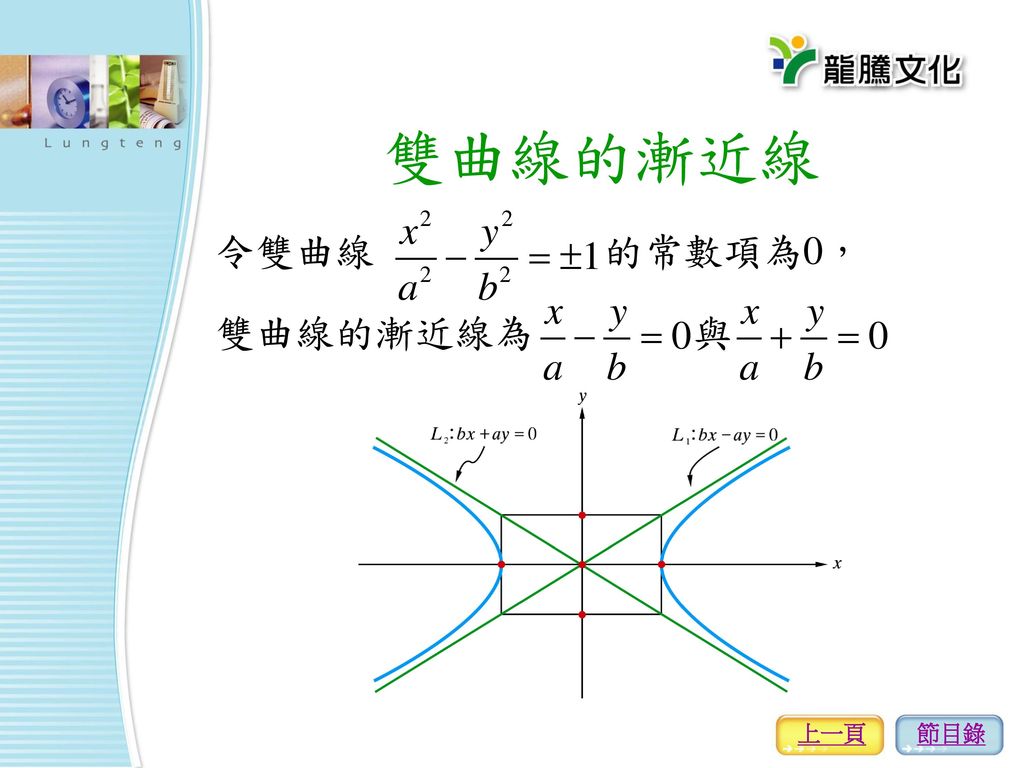



漸近線方程
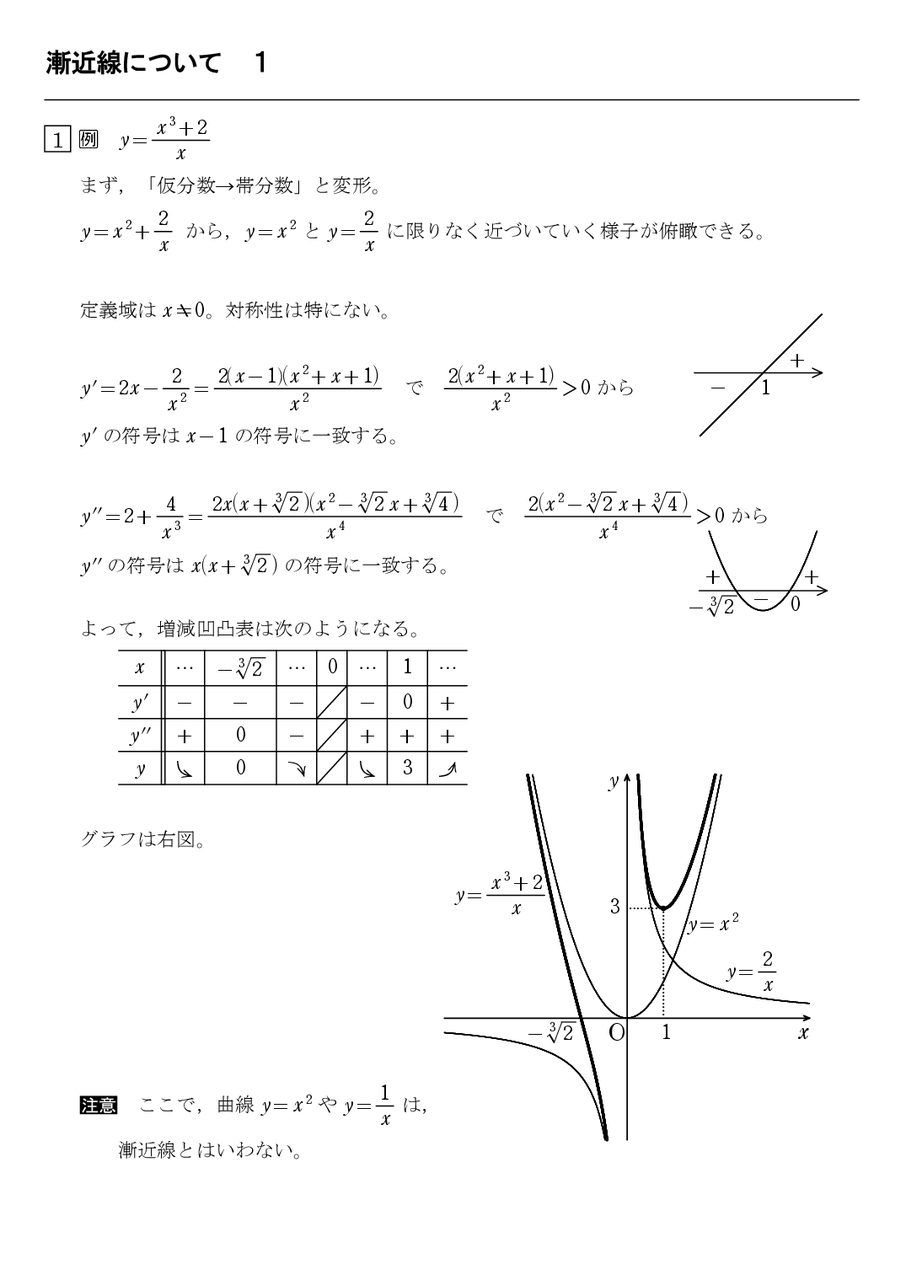



増減凹凸表を書く手順 7 漸近線 1 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線 Op Twitter




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




新入試対応 数学iii基礎問題精講 四訂新装版 Amazon De Bucher




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




漸近線の求め方が分かりません 3 です Clear
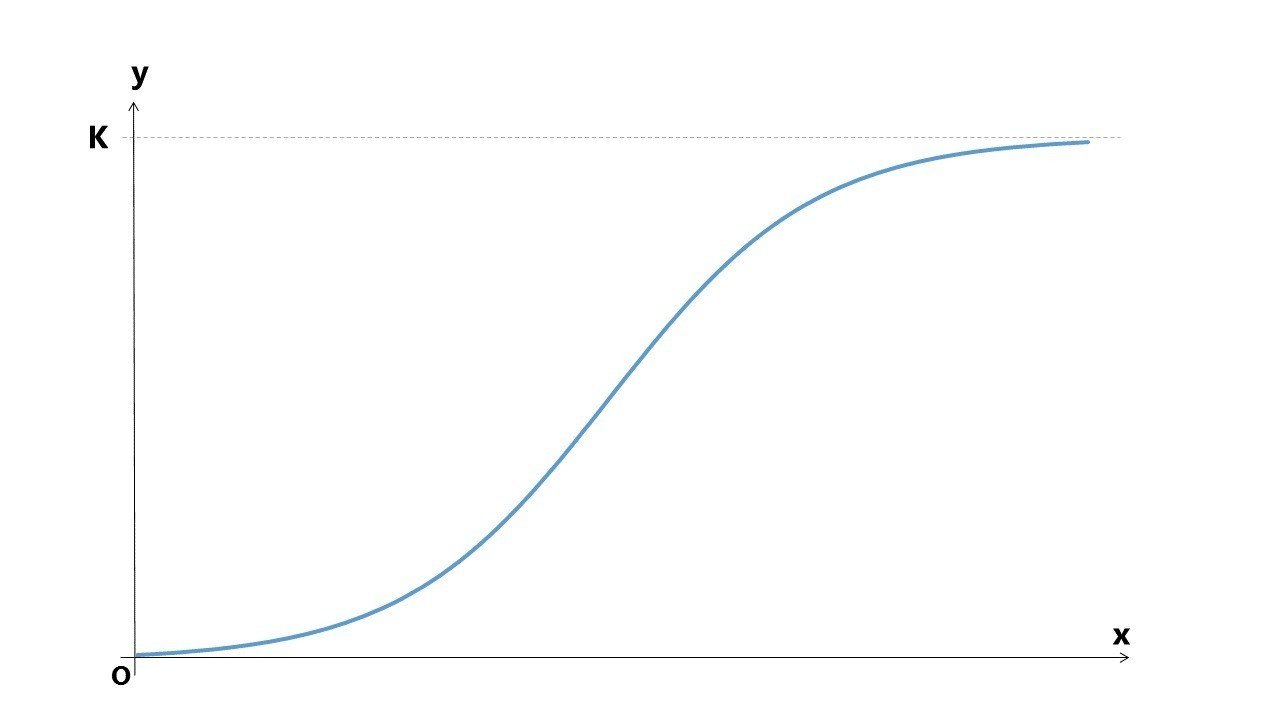



努力と成長に関する数学的考察 その1 大坪 誠 Makoto Otsubo Note



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース
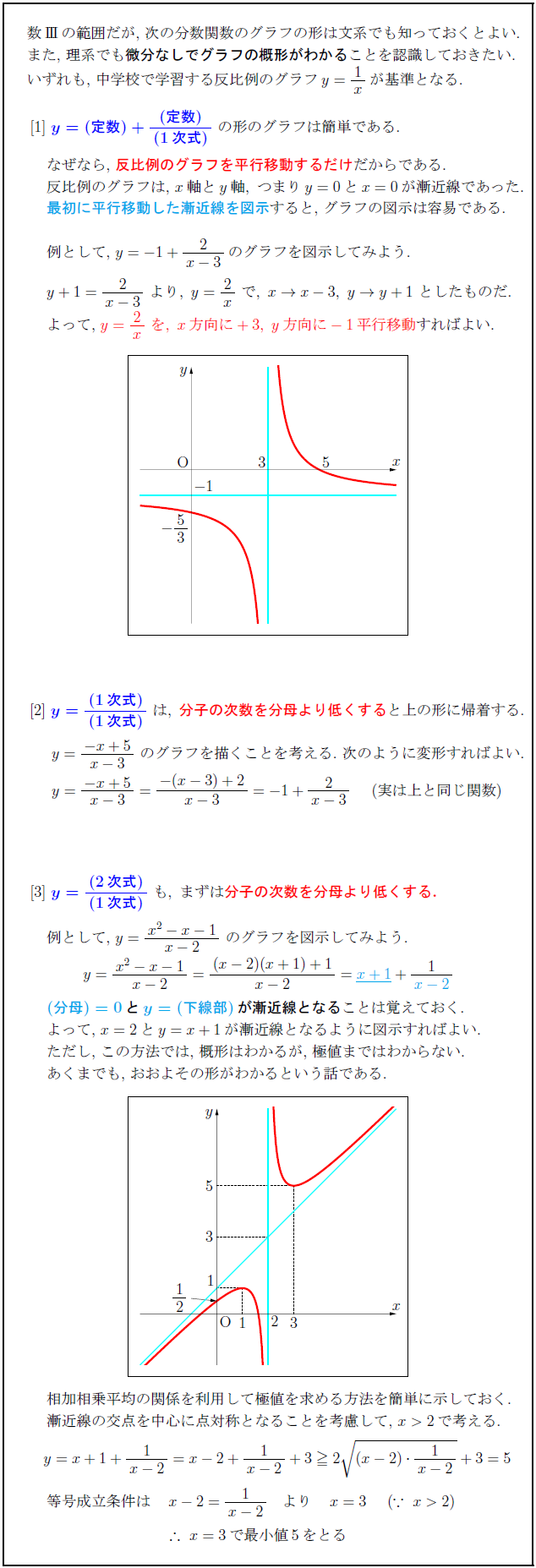



高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月
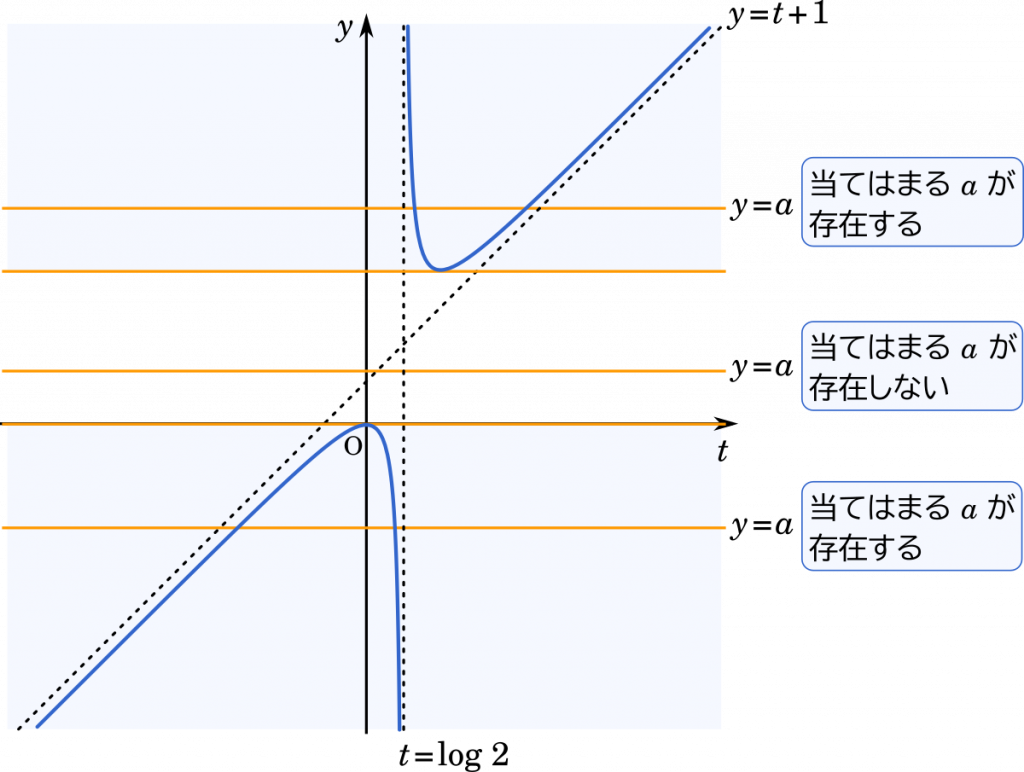



数iii微分 接線の座標の存在範囲 漸近線を求めてグラフの概形を描く 九州大 Mm参考書
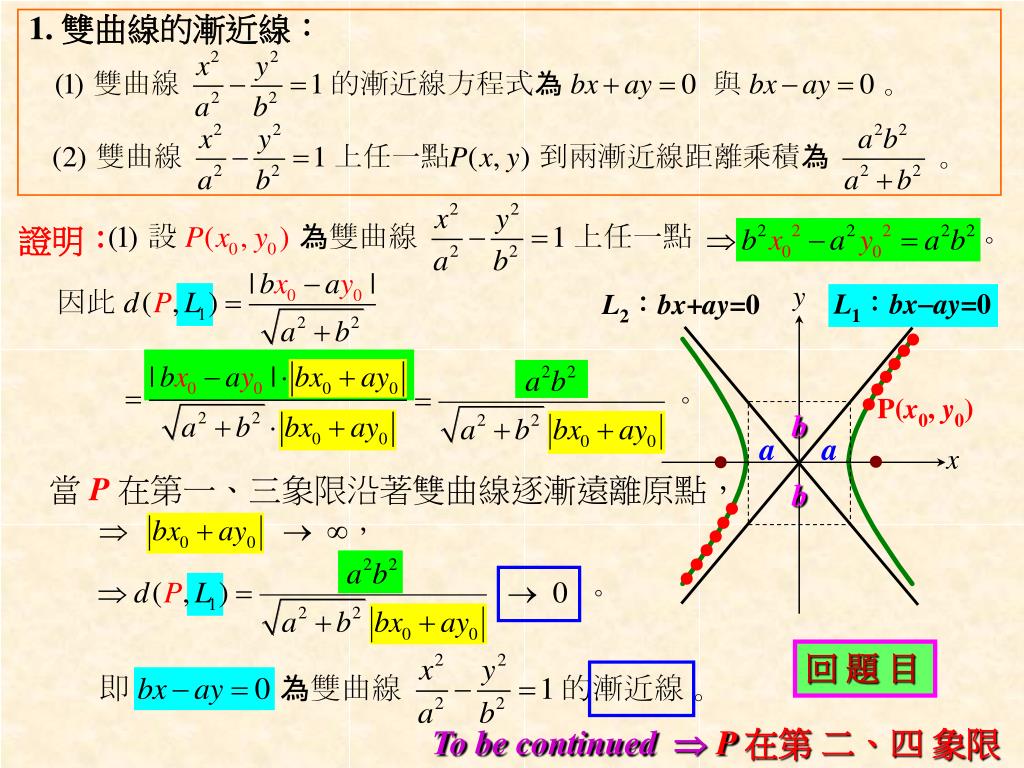



漸近線方程
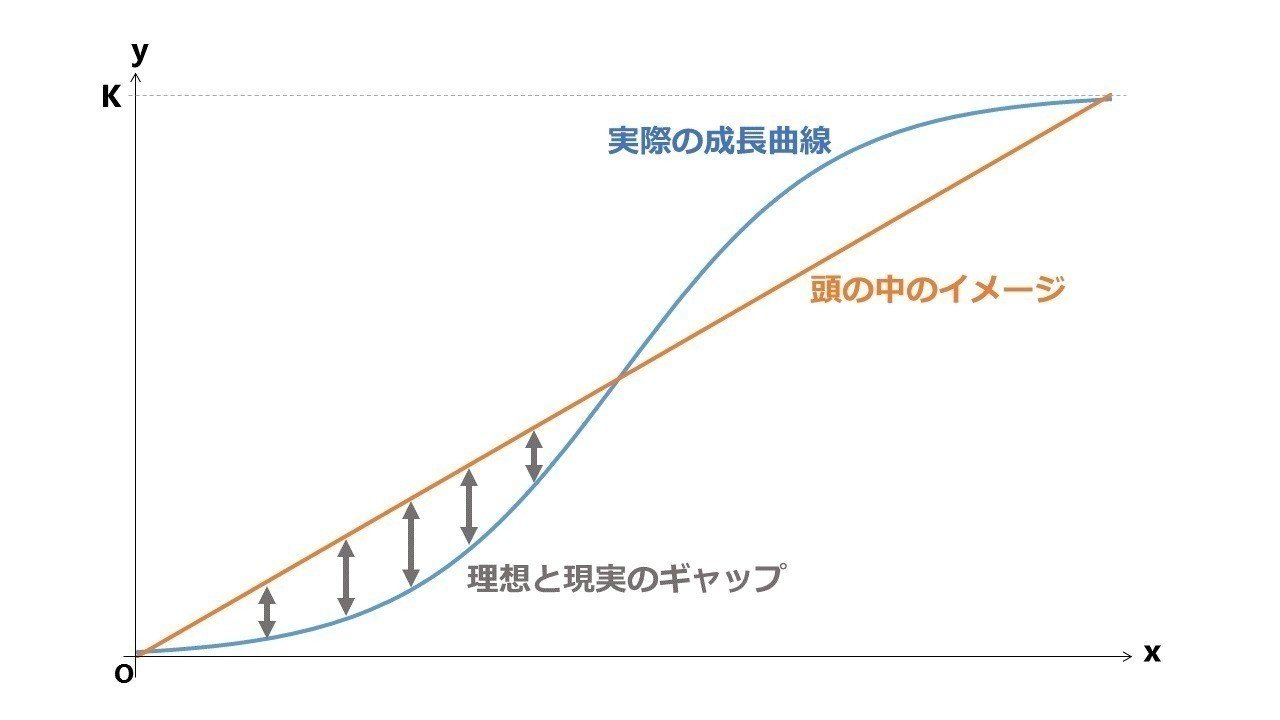



努力と成長に関する数学的考察 その1 大坪 誠 Makoto Otsubo Note




高校数学 2次曲線の決定 2 問題編 映像授業のtry It トライイット




F X 1 Dfrac4x2dfracx2 4x Descubre Como Resolverlo En Qanda




この問題でy 0 を求めないのは何故ですか Clear




数 関数 分数関数 平行移動 漸近線 オンライン無料塾 ターンナップ Youtube
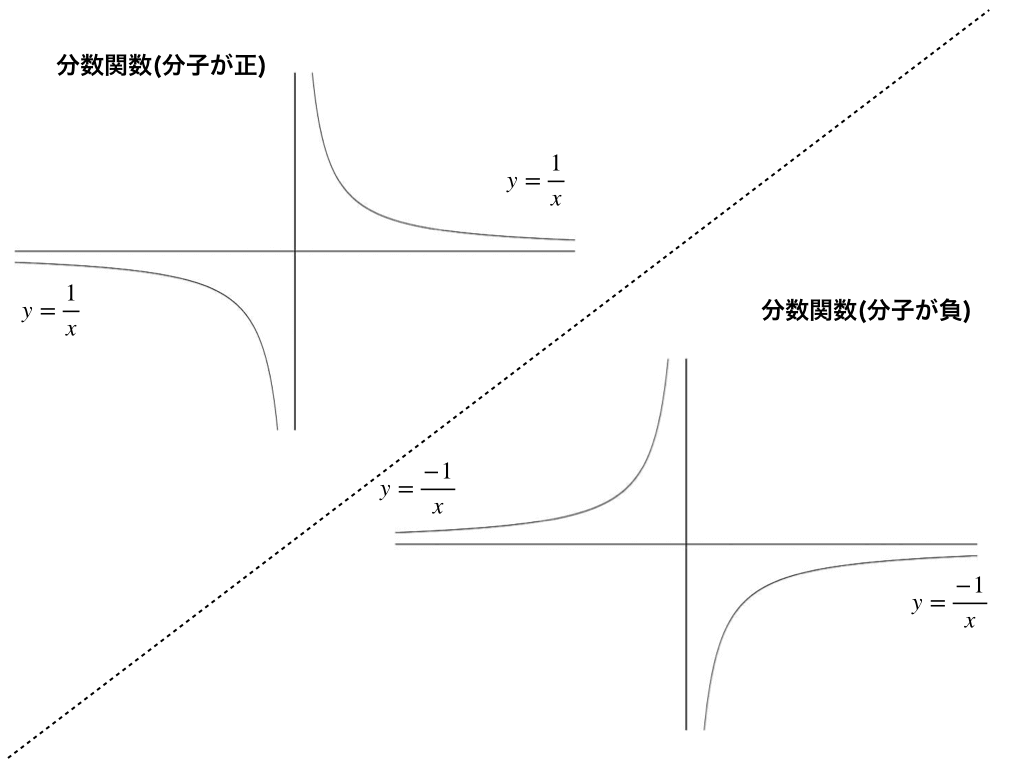



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




二次曲線とは 双曲線の方程式の考え方と書き方 高校数学の知識庫




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




高校数学 双曲線のグラフ 1 映像授業のtry It トライイット



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




漸近線 問題編 1 数 微分法 現大手予備校講師の5分でわかる 高校数学 Youtube




漸近線 Op Twitter



漸近 線 と は 数 微分の応用 ざっくりイメージから漸近線を導く



ストロフォイド ぽじぽめの部屋



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




高校数学 分数関数のグラフ 1 映像授業のtry It トライイット




漸近線 Wikipedia




ロジスティック方程式 Wikipedia



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
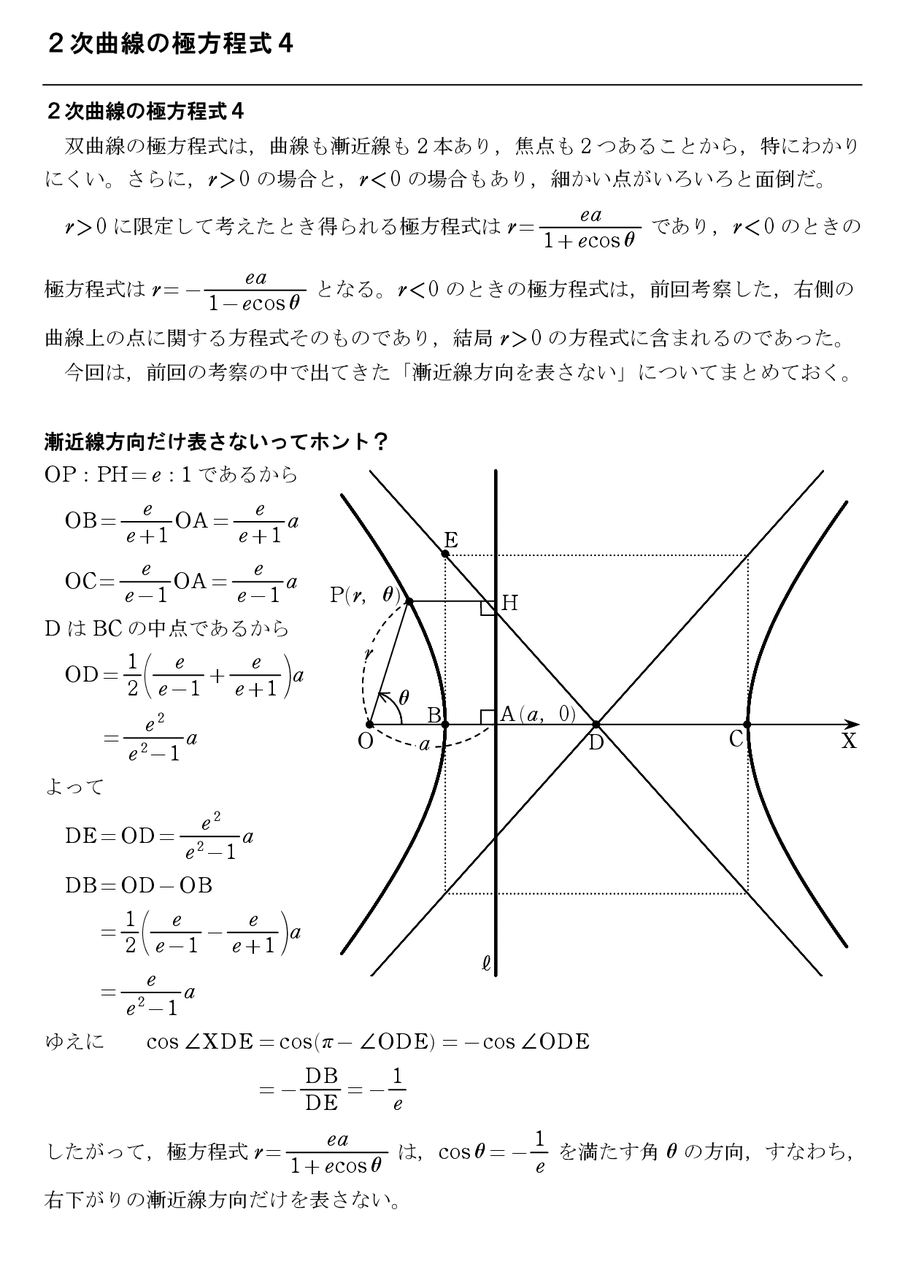



2次曲線の極方程式4 怜悧玲瓏 高校数学を天空から俯瞰する



漸近線方程
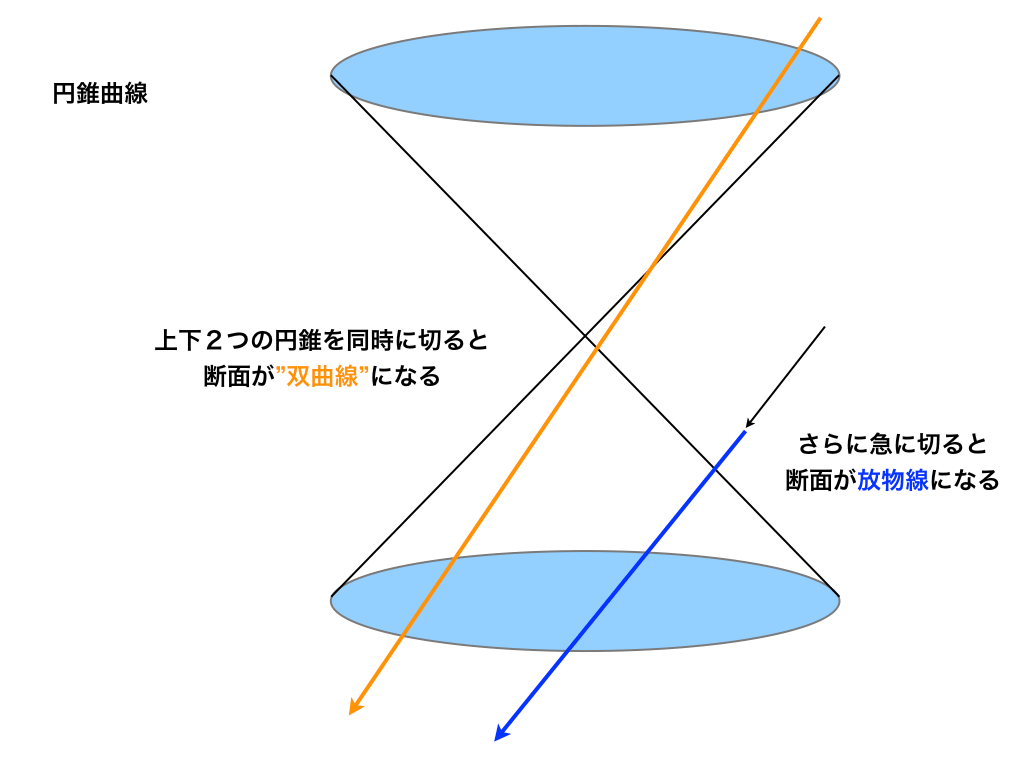



双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説




漸近線方程



誤答から学ぼうシリーズ 陰関数表示と曲線の概形 ほのぼの数学頑張ろう
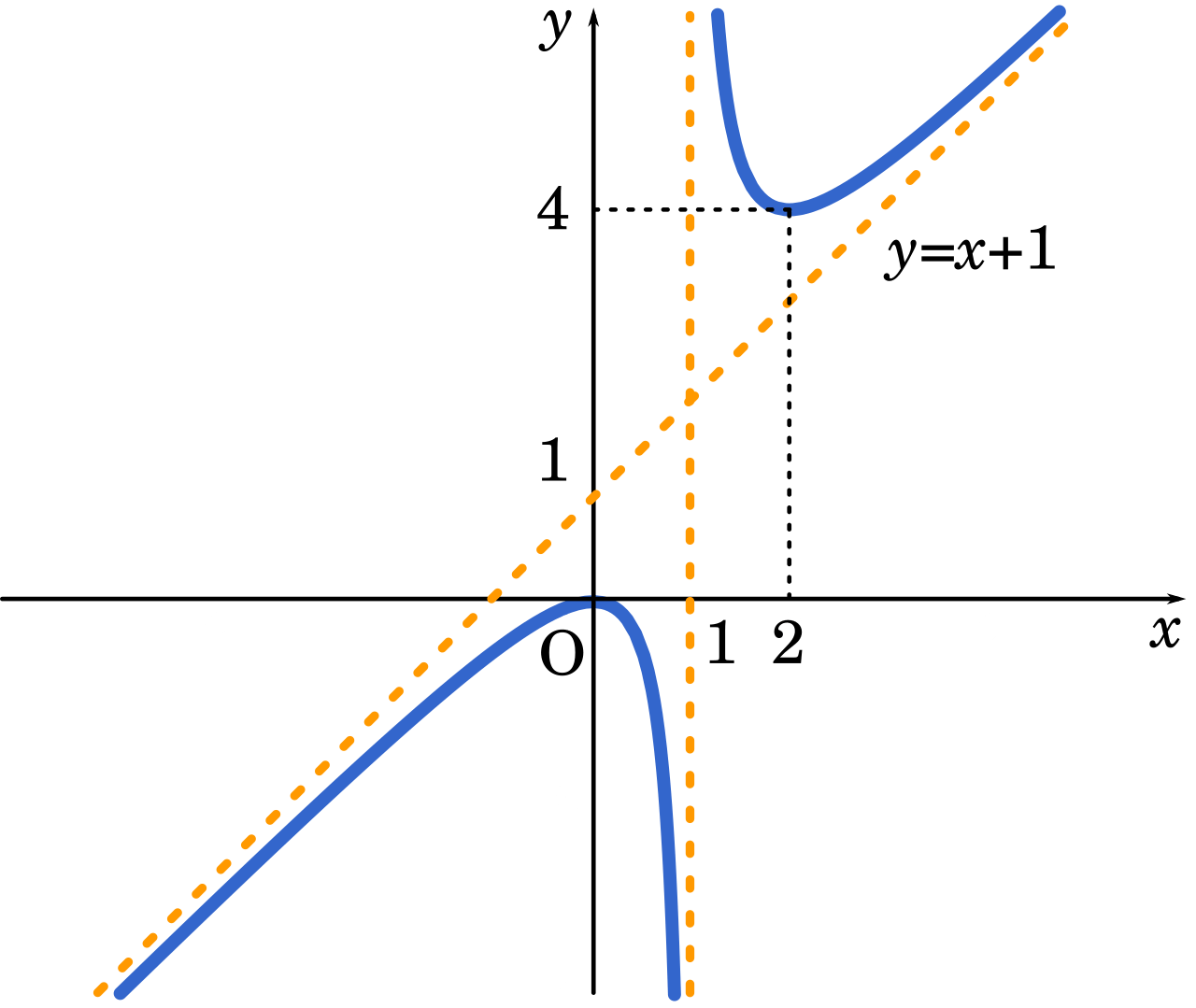



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



My Math Note



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典
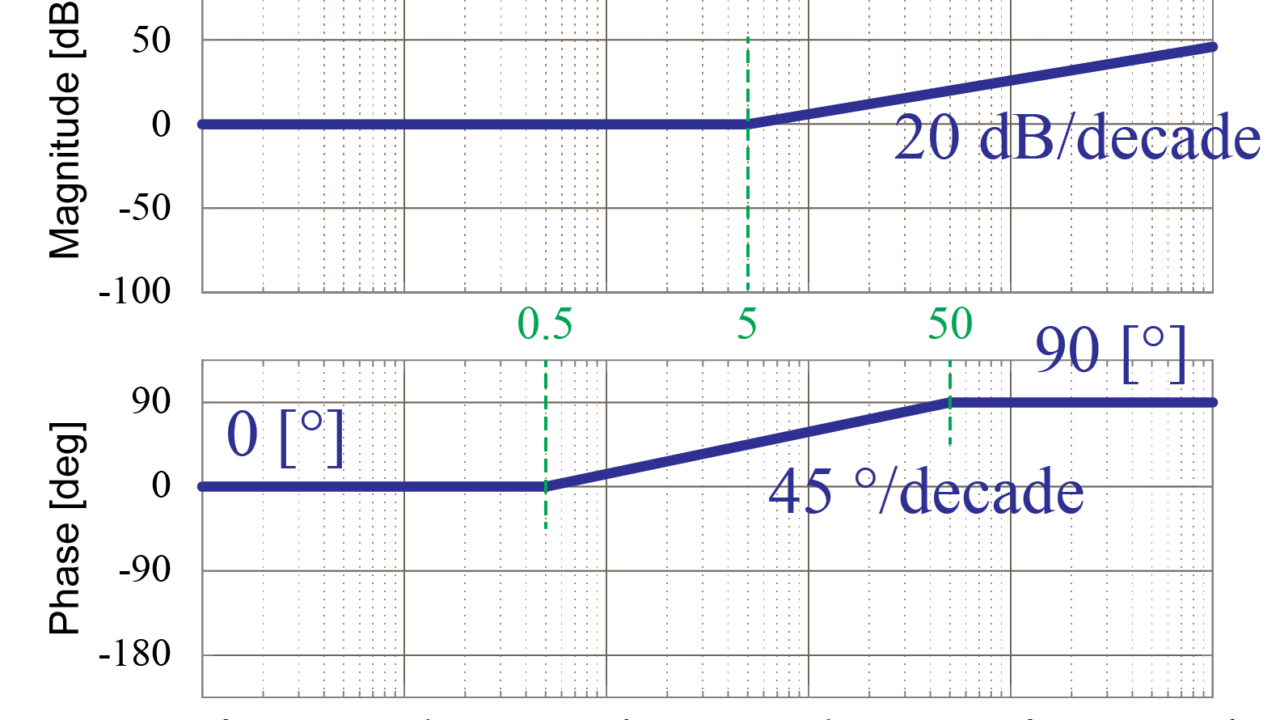



実際に伝達関数からボード線図を漸近線近似で書いてみよう その2 Tajima Robotics



0 件のコメント:
コメントを投稿